二分搜與並查集

二分搜

你要搜尋的東西有單調性(遞增、遞減之類的)

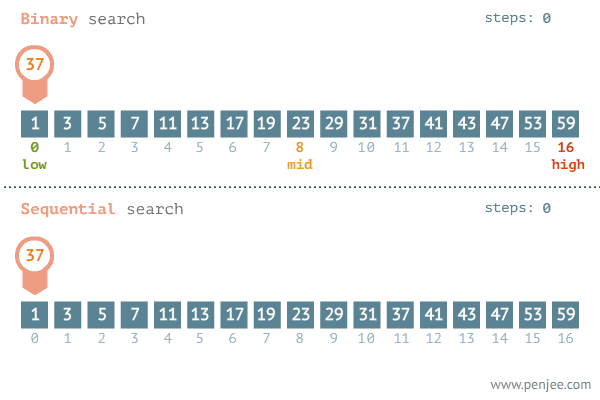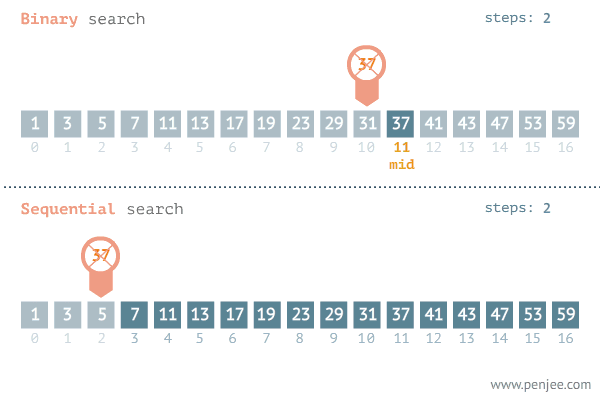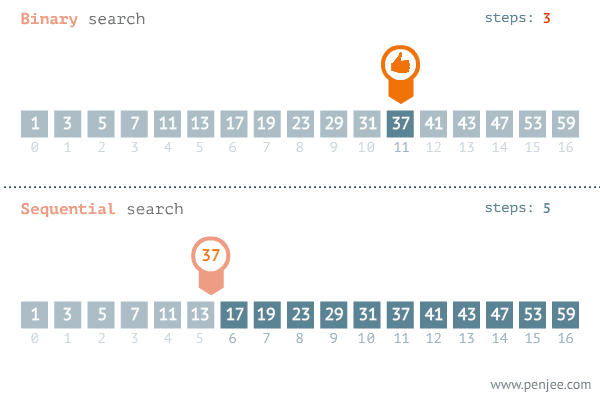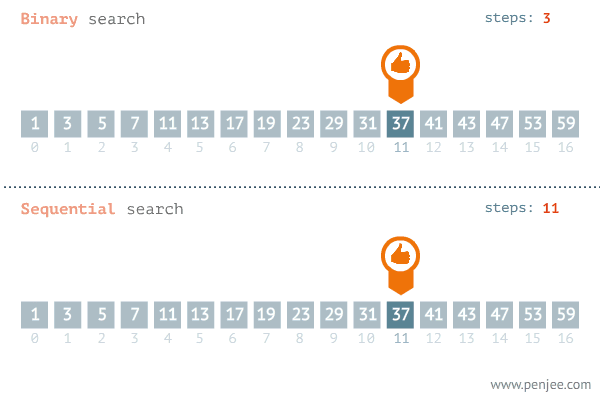
用以搜尋已排序的一串資料。其原理為將欲搜尋的值，與搜索範圍的中間值做比對。

若是搜尋值與中間值不同，且搜尋值比中間值為大。由於資料有單調性，我們可以得知：中間值以前的資料全都比搜尋值還小，所以我們就不需要再浪費時間搜尋這個範圍的值。

相反的，若是搜尋值比中間值為小，我們也可以得知：中間值以後的資料全都比搜尋值還大，也代表接下來我們不需要去尋找中間值以後的值。

接著，由於搜尋到資料的可能範圍僅剩下一半。我們運用同樣的方式，取出這個範圍資料的中間值與搜尋值做比對。再依據此中間值將資料分成兩半，直到找到搜尋值為止。

題目當然不會給你陣列讓你搜啊，通常都是答案有單調性，必須要用二分搜去查找答案所在

兩隻惡魔

題目在這裡
這題其實用deque是可以做的喔，知道我在說什麼的就來吧！