\(
\newcommand{\ord}[1]{\mathcal{O}\left(#1\right)}
\newcommand{\abs}[1]{\lvert #1 \rvert}
\newcommand{\floor}[1]{\lfloor #1 \rfloor}
\newcommand{\ceil}[1]{\lceil #1 \rceil}
\newcommand{\opord}{\operatorname{\mathcal{O}}}
\newcommand{\argmax}{\operatorname{arg\,max}}
\newcommand{\str}[1]{\texttt{"#1"}}
\)
「互斥集」的意思是一組不相交的動態集合
\(S=\{S_1,S_2,...,S_k\}\)
大家擁有的元素都不相同
也就是說這些集合們之間都沒有交集。
每個集合通過一個代表來識別,代表即集合中的某個成員。
在某些應用中,哪一個成員被選作代表是無所謂的;
在另一些應用中,如何選擇代表可能有預先說明的規則,例如選擇集合的最小元素。
如此就可以輕易地維護disjoint-set了
讓我們先來看看code吧
MAKE_SET很明顯是\(\ord{1}\)
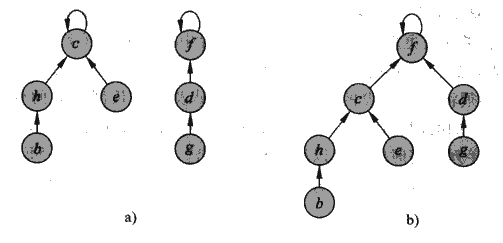
在FIND_SET查找時,使查找路徑上每個點的父母節點指標都指向根節點,如下圖中所示,他非常簡單而有效
原始的樹為圖a,FIND_SET(\(a\))後的結果為圖b
可以得到最壞情況運行時間為:
\(\theta(n+f*(1+log_{2+f/n}n)\;)\)
這裡就不證明了
在資訊競賽中,這樣的複雜度就夠好了
而且並查集的常數很小,幾乎跟線性差不多
簡單的來說就是每個集合維護其元素的個數
UNION的時候把個數比較小的那棵樹的根的父母節點指標指向個數比較多的那棵樹的根
可以得到最壞情況運行時間為:
\(\ord{n+f*log_2 n}\)
如果兩個優化一起使用的話,不就更快了?
$$ A(k,j)=\left \{ \begin{aligned} j+1, && if \; k=0 \\ A(k-1,1), && if \; k>0 \; and \; j=0 \\ A(k-1,A(k,j-1)), && if \; k>0 \; and \; j>0 \end{aligned} \right. $$
這是一個急速成長的函數,為了說明這個函數有多快,以下提供一些例子
$$ \alpha(n)=min(\{k:A(k,1)≥n\}) $$ 很明顯的在正常情況下\(\alpha(n)≤4\)
有人證明了兩種優化一起使用的均攤複雜度為:
$$\ord{m \alpha(n)}$$
Disjoint-set 並查集
南天門日月卦長
Disjoint-set
\(S=\{S_1,S_2,...,S_k\}\)
大家擁有的元素都不相同
也就是說這些集合們之間都沒有交集。
A = {1, 3, 7, 8}
B = {4, 5}
C = {2}
\(S\) = {A, B, C}構成Disjoint sets。
D = {1, 2, 3}
\(M\) = {A, B, C, D}不是Disjoint sets。
B = {4, 5}
C = {2}
\(S\) = {A, B, C}構成Disjoint sets。
D = {1, 2, 3}
\(M\) = {A, B, C, D}不是Disjoint sets。
\(S\) = {A, B, C}
A = {1, 3, 7, 8},選1作為代表
B = {4, 5},選5作為代表
C = {2},選2作為代表
A = {1, 3, 7, 8},選1作為代表
B = {4, 5},選5作為代表
C = {2},選2作為代表
程式不會記錄集合的名子,只記錄集合的代表
並查集的操作
MAKE_SET(x)
建立一個集合,其唯一的成員就是x。因為各集合是不相交的,所以要求x沒有在其它集合中出現過。
UNION(x,y)
將包含x,y的動態集合(例如\(S_x,S_y\))合併為一個新的集合。
假定在這個操作之前兩個集合是不相交的。
再經過此操作後,所得的集合代表可以是\(S_x∪S_y\)中的任何成員,
但在UNION的很多實作中,都是選擇\(S_x\)或\(S_y\)的代表作為新的代表。
由於要求集合是不相交的,故我們"消除了"集合\(S_x,S_y\),把他們從\(S\)中刪去。
FIND_SET(x)
返回一個指標,指向包含x的集合代表
disjoint-set forest
並查集森林
並查集森林
用有根樹來代表集合,樹中的每個節點都分別代表集合的一個成員,每棵樹表示一個集合,集合代表為樹根
MAKE_SET創建一顆僅包含一個節點的樹
執行FIND_SET時,沿著父母節點的指標一直找下去,直到找到樹根為止
UNION操作把一棵樹樹根的父母節點指標指向另一棵樹的樹根,如圖b所示
執行FIND_SET時,沿著父母節點的指標一直找下去,直到找到樹根為止
UNION操作把一棵樹樹根的父母節點指標指向另一棵樹的樹根,如圖b所示
讓我們先來看看code吧
很慢的code
時間複雜度
設n是集合中元素的個數MAKE_SET很明顯是\(\ord{1}\)
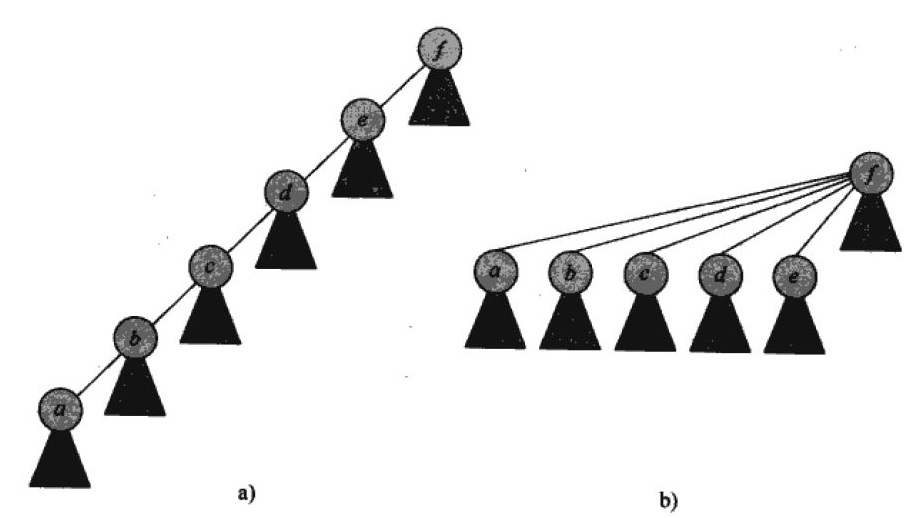
但是當樹為一條鏈時
FIND_SET的複雜度為\(\ord{n}\)
UNION最差複雜度也是\(\ord{n}\)
太慢了!
兩種優化
路徑壓縮
複雜度
如果有n個MAKE_SET操作,f個FIND_SET操作的話可以得到最壞情況運行時間為:
\(\theta(n+f*(1+log_{2+f/n}n)\;)\)
這裡就不證明了
而且並查集的常數很小,幾乎跟線性差不多
啟發式合併
UNION的時候把個數比較小的那棵樹的根的父母節點指標指向個數比較多的那棵樹的根
複雜度
很明顯的,假設樹的大小為n,則樹的高度不會超過\(log_2 n\)
這非常容易理解所以就不說明了
FIND_SET最差只會走過樹上由根到葉節點的一條路徑
也就是 FIND_SET的複雜度\(≤\ord{樹的高度}\)
可以得到最壞情況運行時間為:
\(\ord{n+f*log_2 n}\)
兩種優化一起使用
這兩個方法都可以讓速度變快如果兩個優化一起使用的話,不就更快了?
Ackermann function and their inverse
阿克曼函數與其反函數
定義
Ackermann function$$ A(k,j)=\left \{ \begin{aligned} j+1, && if \; k=0 \\ A(k-1,1), && if \; k>0 \; and \; j=0 \\ A(k-1,A(k,j-1)), && if \; k>0 \; and \; j>0 \end{aligned} \right. $$
定理
Ackermann function
對於任意正整數\(j≥1\),有\(A(1,j)=2j+1\)
對於任意正整數\(j≥1\),有\(A(2,j)=2^{j+1}(j+1)-1\)
\(A(3,1)=A(2,A(2,1))=A(2,7)=2047\)
\(A(4,1)=A(3,A(3,1))=A(3,2047)\gg A(2,2047)\)
\(\qquad =2^{2048}*2048-1\gg 10^{80}\)
定義
Inverse of Ackermann function$$ \alpha(n)=min(\{k:A(k,1)≥n\}) $$ 很明顯的在正常情況下\(\alpha(n)≤4\)
兩種優化一起使用
假設MAKE_SET、UNION、FIND_SET共有m次操作有人證明了兩種優化一起使用的均攤複雜度為:
$$\ord{m \alpha(n)}$$
正常情況下\(\alpha(n)≤4\)
已經是常數時間了,超級快!
已經是常數時間了,超級快!