一般圖最大權匹配

general graph weighted match

南天門日月卦長

甚麼是匹配?

匹配(最大邊獨立集)

一張圖$G=(V,E)$，這張圖的一個匹配$M$是邊集$E$的一個子集，其中每兩條邊都不相鄰（沒有公共頂點）

最大匹配

圖$G$的一個 最大匹配 ，指邊數最多的匹配。

最大匹配 可能有不止一個，但 最大匹配 的邊數是確定的，並且不可能超過圖中頂點數的一半。

完美匹配

圖$G$的 最大匹配 包含所有原圖的所有點，稱為 完美匹配
若$G$為完全圖且頂點數為偶數時，必然存在 完美匹配

最大權匹配

maximum weight matching

一張圖$G=(V,E)$
$\forall e \in E$存在一個函數$w(e)$表示$e$的權重

圖$G$的一個 最大權匹配 $M=(V',E')$是圖$G$的一個子圖
滿足$ \sum w(e): e \in E'$為其所有匹配中最大的

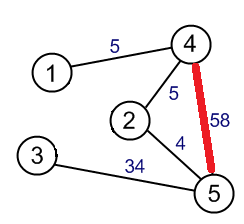
最大權最大匹配

maximum weight maximum cardinality matching

圖$G$的一個 最大權最大匹配 $M=(V',E')$
滿足$ \sum w(e): e \in E'$為其所有 "最大匹配" 中最大的

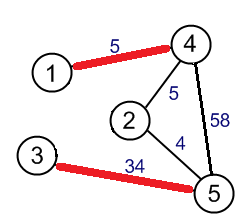
最大權完美匹配

maximum weight maximum perfect matching

若圖$G$存在完美匹配
此時圖$G$的 最大權最大匹配 稱為 最大權完美匹配

匹配算法的轉換

最大權最大匹配 允許負權邊$(w(e)<0)$
但是 最大權匹配 不會有負權邊

若一張圖$G$其所有的邊皆為負權
則其 最大權匹配 $M=\varnothing$

調整邊的權重

先將圖$G$的所有負權邊其權重$w(e)$設為$0$
在進行接下來的步驟

完全圖性質

在$G$為完全圖且沒有負權邊時

最大權最大匹配 = 最大權匹配

所以把$G$補成完全圖，補上的邊其權重為$0$
計算 最大權最大匹配 後再把權重為$0$的邊去除即可

最大權匹配 不會有負權邊
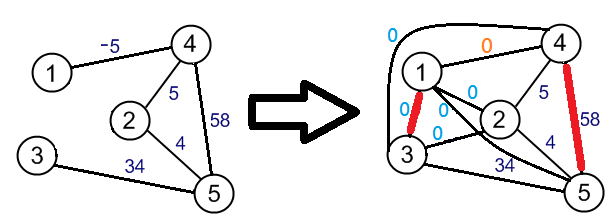
且零邊$ (w(e)=0) $可選可不選
但是 最大權最大匹配 允許負權邊和零邊

調整邊的權重

令 $K = max(\{\abs{w(e)}: e \in E ,\; w(e) ≤ 0 \}) + 1 $

若沒有負權邊或零邊則$K = 0$

調整邊的權重

把圖$G$中所有的邊其權重$w(e)$加上$K$產生一張新圖$G'=(V,E')$

此時的新圖$G'$不存在負權邊和零邊

問題來了

最大權最大匹配 不一定等於 最大權匹配
但是把所有邊的邊權加上一個超大數字$P$的話
最大權匹配 的結果就是 最大權最大匹配

但是$P$取要多大?

調整邊的權重

令$P = \sum{w(e): e \in E'}$

把圖$G'$中所有的邊其權重$w(e)$加上$P$
產生一張新圖$G''=(V,E'')$

此時對圖$G''$進行 最大權匹配
其結果可以對應原圖的 最大權最大匹配

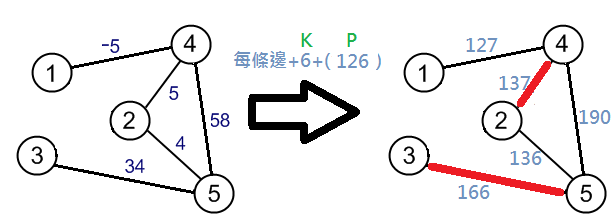
最大匹配算法

flow

最簡單的方法是用網路流，所以就不多講了
Dinic在這種特殊圖上複雜度為$ \ord{|E|\sqrt{|V|}} $

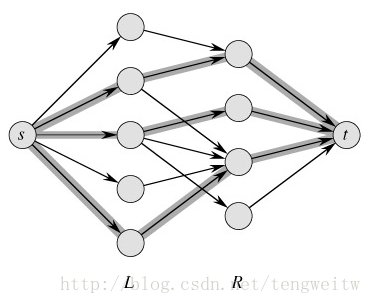
交錯樹

alternating tree

在進行DFS或BFS尋找增廣路的過程產生的樹稱為交錯樹
設 $T=(V_t,E_t)$為在尋找增廣路時產生的交錯樹
定義:
偶點為樹上深度為偶數的點
奇點為樹上深度為奇數的點

Berge's Theorem

定理

Berge's Theorem

從圖上任取一個未匹配點，如果找不到以此點作為端點的增廣路，那麼這張圖會有一些最大匹配不會包含此點。

接下來我們要來證明Berge's Theorem

對稱差集

定義

對稱差集

兩個集合 $A$ 和 $B$ 的「對稱差集」定義為
$A⊕B = (A∪B) - (A∩B)$

同一張圖上的兩種匹配$M$和$M^*$也可以計算對稱差集

$M⊕M^*$總共會產生六大類 connected component

設當下的匹配$M$找不到以未匹配點$p$作為端點的擴充路徑
並令$M^*$是該圖的其中一個最大匹配。

如果$p$不在$M^*$上

證明

Berge's Theorem

$p$不在$M^*$上定理成立。

如果$p$在$M^*$上

證明

Berge's Theorem

1. $p$對於M來說是未匹配點。理所當然$p$不在$M$上。
2. 考慮$M⊕M^*$的六種情形。$p$不在$M$上，且$p$在$M^*$上，所以只有d或e符合條件。
3. $M$找不到以$p$作為端點的擴充路徑，所以d不符合條件，只有e符合條件。
4. 對於$M^*$來說，只要照著e顛倒匹配邊和未匹配邊，就可以製造出另一個不會包含p的最大匹配，成為1.的情形，定理還是成立。

結論:Berge's Theorem是正確的

匈牙利算法

複雜度

總共做了$n1$次dfs
每次dfs花了$ \ord{|E|+n2+n1} $的時間
總複雜度為$ \ord{n1*(|E|+n2+n1)} $

匈牙利算法

多重匹配

這種問題的題目通常是這樣

給一張圖G有n1個點和n2個點，n1個點之間沒有邊，n2個點之間也沒有邊，但是n1和n2個點之間有m條邊(簡單的來說就是n1個點和n2個點的二分圖啦)，沒有重邊；其中n2個點每個點u都有一個可接受匹配數$c_u$。 n1的點只能跟一個點匹配，但n2的點在不超過可接受匹配數的情況下，可以跟多個點匹配，求這張圖的最大匹配

這依然可以用普通的匈牙利演算法來解決
把可以多重匹配的點拆開，能匹配幾次就拆成幾個點
設n2個點每個點$u$都有一個值$E_u$表示和$u$相鄰的邊數
複雜度$\ord{n1*(\sum{c_u*E_u}+n1+n2)}$
但是空間複雜度為$\ord{\sum{c_u*E_u}+n1+n2}$

可以利用vector存每個點對那些點有匹配
雖然時間複雜度不變
但是效能變快了
空間複雜度也會和一般的匈牙利一樣

這樣基本問題就解決了，來計算一下時間複雜度

因為一朵花最少有三個點，縮花後成為一個點
由此推得：N個點的圖建立一棵交錯樹，最多縮花N/2次

所以找出增廣路的時間複雜度為:
$ \ord{|E|+|V|} + \ord{|E|+|V|} = \ord{|E|+|V|} $
BFS的時間加上縮花總時間

複雜度分析

之前有討論過bfs加上縮花的時間為$\ord{|E|+|V|}$
總共會進行$|V|$次bfs

故總複雜度為$ \ord{|V|*(|E|+|V|)} $

定義函數

設$S ⊆ V$
$δ(S) = \{ (u, v) ∈ E \; : \; u ∈ S, \; v ∈ V − S \} $
對單一點 $v ∈ V $ ，我們定義 $δ(v) = δ(\{v\}) $

二分圖最大權完美匹配的線性規劃

原始問題

PRIMAL

$ max \; \sum_{e∈E} \; w(e)x_e $

限制:
$x_e ≥ 0 \; : \forall e∈E $
$ x(δ(u)) = 1 \; : \forall u∈V $

定義:
$x(S) = \sum_{e∈S} \; x_e$

接下來進行對偶問題的轉換

二分圖最大權完美匹配的對偶問題

對偶問題

DUAL

$ min \; \sum_{u \in V} \; z_u $

限制:
$z_e ≥ 0 \; : \forall e∈E $

設 $e=(u,v)$，這裡$z_e = z_u + z_v - w(e)$

所有條件都滿足時$\sum_{u∈V} \; z_u$就是最大權匹配的權重和

原本求最大值問題就變成求最小值了!

二分圖最大權完美匹配的對偶問題

在原始問題中，我們發現只要在$x_e \in \{0,1\} \; : \forall e \in E $時
$x_e = 1$的邊就是匹配邊，$x_e = 0$的邊就是非匹配邊

不過線性方程的解中，$x_e$不一定是整數
但是一定存在$x_e \in \{0,1\}$的整數解
所以想辦法讓他產成整數解即可

二分圖最大權完美匹配的對偶問題

我們稱$z_u$為u的vertex labeling
稱$z_e=0$的邊為等邊(Equality Edge)

只要在最大權完美匹配的時候
讓所有匹配邊都是等邊
這樣就可以滿足$x_e \in \{0,1\}$的條件了

寫成數學符號長這樣

$x_e>0 \; \longrightarrow \; z_e=0 \qquad \forall e \in E$

以「等邊」的概念，結合之前的匈牙利算法:

用「等邊」構成的增廣路不斷進行擴充
由於用來擴充的邊全是「等邊」
最後得到的最大權完美匹配當然全是「等邊」

找不到「等邊」?只好調整vertex labeling了

調整 vertex labeling

vertex labeling 仍要維持大於等於的性質
而且既有的「等邊」不能被改變。

調整 vertex labeling

調整

vertex labeling

設交錯樹 $ T = (U_t,V_t) $
令 $ d = min(\{z_e : e \in δ(V_t)\})$
設$u^+$為樹上偶點，$v^-$為樹上奇點
讓 $z_{u^+}$-= $d, \;$$z_{v^-}$ += $d$

如此便製造了一條(以上)的等邊，且既有等邊保持不動
並維持了$z_e ≥ 0 \; : \forall e∈E $的性質
接著就繼續找增廣路!

因為是二分圖
所以可以事先知道哪些點是奇點
哪些點是偶點

我們一開始的時候可以設定:
所有$u$為偶點，$z_u=max(\{w(e): e \in E\})$
所有$v$為奇點，$z_v=0$

如果要做最大權二分匹配

vertex labeling 額外增加一個限制：
對於所有匹配點$z_u > 0$

一開始先設所有$z_u=max(\{w(e): e \in E\})/2$
vertex labeling為 0 的點最後將成為未匹配點

實作也不會太難大家可以試試看

KM演算法

Kuhn-Munkres algorithm

這個算法可以求二分圖的最大權完美匹配

code

複雜度分析

複雜度

KM演算法

dfs花$\ord{|V|^2}$的時間

因為交錯樹最多有$|V|-1$條邊
故主程式裡的無限迴圈最多執行$\ord{|V|}$次

總共有$|V|$個點需要被增廣

總複雜度為:
$\ord{|V|*|V|*|V|^2}=\ord{|V|^4}$

還可以更好

複雜度

KM演算法

其實這算法複雜度可以到$\ord{|V|^3}$
$\implies$每次增加新的等邊後不需要重新DFS

怎麼實作具體就留給你們吧

一般圖最大權匹配

定義

設$S⊆V$
$ \gamma(S)= \{(u,v) \in E \; : \; u \in S, \; v \in S\} $
$ O = \{ B⊆V \; : \; |B|是奇數且|B|≥3 \} $

一般圖最大權完美匹配的線性規劃

原始問題

PRIMAL

$ max \; \sum_{e∈E} \; w(e)x_e $

限制:
$ x(δ(u)) = 1 \; : \forall u∈V $
$x(\gamma(B))≤\floor{\frac{|B|}{2}} \; : \forall B \in O$
$x_e ≥ 0 \; : \forall e∈E $

一般圖最大權完美匹配的對偶問題

對偶問題

DUAL

$ min \; \sum_{u \in V} \; z_u + \sum_{B \in O} \; \floor{\frac{|B|}{2}} z_B $

限制:
$z_B ≥ 0 \; : \forall B∈O $
$z_e ≥ 0 \; : \forall e∈E $

設 $e=(u,v)$，這裡$$z_e = z_u + z_v - w(e)+\sum_{\begin{subarray}{l} B \in O \\ u,v \in \gamma(B) \end{subarray}} z_B $$

和二分圖一樣
我們必須滿足$x_e \in \{0,1\} \; : \forall e∈E $
因此必須在最大權完美匹配的時候
讓所有匹配邊都是等邊

這裡等邊的定義為$z_e=0$的邊
和二分圖不同的是，多了$z_B$要處理

$z_B$什麼時候會大於0?

從方程式可以看出
盡量讓$z_B=0$是最好的做法
但在不得已的時候還是要讓$z_B>0$

$z_B$什麼時候會大於0?

在$x(\gamma(B))=\floor{\frac{|B|}{2}}$且$x(δ(B)) = 1$時
讓$z_B>0$就可以了

因為除了在這種情況下
$z_B>0$是沒有意義的

所以可以有以下的對應關係

$x_e>0 \; \longrightarrow \; z_e=0 \qquad \forall e \in E$
$z_B>0 \; \longrightarrow \; x(\gamma(B))=\floor{\frac{|B|}{2}}, \; x(δ(B)) = 1 \qquad \forall B \in O$

可以發現在$z_B>0$時，$B$就會是一朵花

以「等邊」的概念，結合之前的帶花樹算法:

用「等邊」構成的增廣路不斷進行擴充
由於用來擴充的邊全是「等邊」
最後得到的最大權完美匹配當然全是「等邊」

還要處理花的問題

花

遇到花的時候，要把它縮成一個偶點
把花中所有點都設為偶點，並讓他的$z_B=0$

由於縮花後會把花保存起來
直到滿足某些條件才會拆開
所以不能用之前的方法紀錄花

花

如果沒有特別說明
我們之後提到的「點」
都有包含縮花後產生的點

花

因為花也有可能縮成點被加入queue中
且花的數量是不固定的

因此我們不能像之前一樣枚舉每個點看看有沒有增廣路
所以在BFS的時候必須要把所有未匹配點都丟到queue中

這樣會同時產生很多棵交錯樹

總而言之

這個算法可以分成四個部分

GROW 、AUGMENT 、SHRINK 、EXPAND

調整 vertex labeling

vertex labeling 仍要維持大於等於的性質
而且既有的「等邊」不能被改變
還要讓$z_B$盡量的小

定義符號

奇偶點

以$u^-$來表示$u$在交錯樹上為奇點
以$u^+$來表示$u$在交錯樹上為偶點
以$u^{\varnothing}$來表示$u$不再任何一棵交錯樹上

之後所有提到的$B$預設都是花
並同時代表縮花之後的點
花也可以有奇花偶花之分
因此也適用$B^+$、$B^-$、$B^{\varnothing}$等符號

調整 vertex labeling

調整

vertex labeling

設目前有$r$棵交錯樹 $ T_i = (U_{t_i},V_{t_i}) \; : 1≤i≤r$
令
$ d1 = min(\{z_e: e=(u^+,v^{\varnothing})\})$

$ d2 = min(\{z_e: e=(u^+,v^+), \; u^+ \in T_i,\;v^+ \in T_j,\; i≠j\})/2$

$ d3 = min(\{z_{B^-}: B^- \in O\})/2$

注意這裡$B$是縮花之後的點，所以可以有奇偶性

設$d=min(d1,d2,d3)$

調整 vertex labeling

調整

vertex labeling

讓
$ \quad z_{u^+}$ -= $d$
$ \quad z_{v^-}$ += $d$
$ \quad z_{B^+}$ += $2d$
$ \quad z_{B^-}$ -= $2d$

如果出現$z_B = 0\;(d = d3)$
為了防止$z_B < 0$的情況
所以要把這朵花拆了(EXPAND)
拆花後只留下花裡的交替路徑
並把花裡不在交替路徑上的點設為未走訪$(\varnothing)$

expand

調整 vertex labeling

調整

vertex labeling

如此便製造了一條(以上)的等邊，既有等邊保持不動
並維持了$z_e ≥ 0 \; : \forall e∈E $的性質
且最低限度增加了$z_B$
可以繼續找增廣路了!

最大權匹配

剛才的作法找出來的是 最大權完美匹配 啊
我們要求的是 最大權匹配

如果要做最大權匹配

vertex labeling 額外增加一個限制：
對於所有匹配點$u$，$z_u > 0$

一開始先設所有$z_u = max(\{w(e) : e \in E\})/2$
vertex labeling為 0 的點最後將成為未匹配點

這裡使用這種方式實做

一般圖最大權匹配

code

Edmonds' Maximum Weight Matching Algorithm

這裡為了方便實作所以用邊權乘二來計算$z_e$的值
這樣就不會出現浮點數誤差了

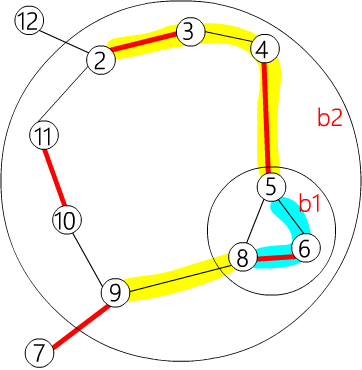
如果你使用get_pr(b2,11)
flower[b2]會變成{9,10,11,2,3,4,b1}
並回傳2

如果你使用get_pr(b2,2)
flower[b2]會變成{9,b1,4,3,2,11,10}
並回傳4

複雜度分析

每朵花在一次BFS中只會被縮花或是拆花一次
每次縮花拆花要$\ord{\abs{V}}$的時間
最多總共有$\ord{\abs{V}}$朵花，故花的處理花費$\ord{\abs{V}^2}$
而BFS花費$\ord{\abs{V}+\abs{E}}$
因此找增廣路花費$\ord{\abs{V}+\abs{E}}+\ord{\abs{V}^2}=\ord{\abs{V}^2}$

複雜度分析

最多做$\abs{V}$次BFS
故總時間複雜度為$\ord{\abs{V}^3}$

題目

二分圖匹配

題目

二分圖匹配

UVA 10080
UVA 670

二分圖多重匹配

題目

二分圖多重匹配

POJ 2289

一般圖匹配

題目

一般圖匹配

UVA 1663

二分圖最大/最小權匹配

題目

二分圖最大/最小權匹配

UVA 1411
UVA 11383

一般圖最大權匹配

題目

一般圖最大權匹配

UOJ 81

參考資料

維基百科

演算法筆記

vfleaking的博客

Blossom V: A new implementation of a minimum cost perfect matching algorithm

Implementation of $\ord{n m \; log \; n}$ Weighted Mathings in General Graphs: The Power of Data Strutures